Every byte and each operation issues when making an attempt to construct a quicker mannequin, particularly if the mannequin is to run on-device. Neural architecture search (NAS) algorithms design subtle mannequin architectures by looking by way of a bigger model-space than what is feasible manually. Different NAS algorithms, comparable to MNasNet and TuNAS, have been proposed and have found a number of environment friendly mannequin architectures, together with MobileNetV3, EfficientNet.
Here we current LayerNAS, an strategy that reformulates the multi-objective NAS drawback throughout the framework of combinatorial optimization to vastly scale back the complexity, which ends in an order of magnitude discount in the variety of mannequin candidates that have to be searched, much less computation required for multi-trial searches, and the invention of mannequin architectures that carry out higher total. Using a search house constructed on backbones taken from MobileNetV2 and MobileNetV3, we discover fashions with top-1 accuracy on ImageNet as much as 4.9% higher than present state-of-the-art options.
Problem formulation
NAS tackles a wide range of completely different issues on completely different search areas. To perceive what LayerNAS is fixing, let’s begin with a easy instance: You are the proprietor of GBurger and are designing the flagship burger, which is made up with three layers, every of which has 4 choices with completely different prices. Burgers style in a different way with completely different mixtures of choices. You wish to take advantage of scrumptious burger you possibly can that comes in beneath a sure price range.
 |
| Make up your burger with completely different choices out there for every layer, every of which has completely different prices and gives completely different advantages. |
Just just like the architecture for a neural community, the search house for the right burger follows a layerwise sample, the place every layer has a number of choices with completely different modifications to prices and efficiency. This simplified mannequin illustrates a standard strategy for organising search areas. For instance, for fashions based mostly on convolutional neural networks (CNNs), like MobileNet, the NAS algorithm can choose between a special variety of choices — filters, strides, or kernel sizes, and so forth. — for the convolution layer.
Method
We base our strategy on search areas that fulfill two situations:
- An optimum mannequin may be constructed utilizing one of many mannequin candidates generated from looking the earlier layer and making use of these search choices to the present layer.
- If we set a FLOP constraint on the present layer, we will set constraints on the earlier layer by decreasing the FLOPs of the present layer.
Under these situations it’s attainable to search linearly, from layer 1 to layer n figuring out that when looking for the most suitable choice for layer i, a change in any earlier layer is not going to enhance the efficiency of the mannequin. We can then bucket candidates by their price, in order that solely a restricted variety of candidates are saved per layer. If two fashions have the identical FLOPs, however one has higher accuracy, we solely preserve the higher one, and assume this received’t have an effect on the architecture of following layers. Whereas the search house of a full remedy would develop exponentially with layers because the full vary of choices can be found at every layer, our layerwise cost-based strategy permits us to considerably scale back the search house, whereas having the ability to rigorously purpose over the polynomial complexity of the algorithm. Our experimental analysis reveals that inside these constraints we’re capable of uncover top-performance fashions.
NAS as a combinatorial optimization drawback
By making use of a layerwise-cost strategy, we scale back NAS to a combinatorial optimization drawback. I.e., for layer i, we will compute the fee and reward after coaching with a given part Si . This implies the next combinatorial drawback: How can we get the most effective reward if we choose one alternative per layer inside a price price range? This drawback may be solved with many various strategies, one of the easy of which is to make use of dynamic programming, as described in the next pseudo code:
whereas True: # choose a candidate to search in Layer i candidate = select_candidate(layeri) if searchable(candidate): # Use the layerwise structural data to generate the youngsters. youngsters = generate_children(candidate) reward = prepare(youngsters) bucket = bucketize(youngsters) if memorial_table[i][bucket] < reward: memorial_table[i][bucket] = youngsters transfer to subsequent layer |
| Pseudocode of LayerNAS. |
 |
| Illustration of the LayerNAS strategy for the instance of making an attempt to create the most effective burger inside a price range of $7–$9. We have 4 choices for the primary layer, which ends in 4 burger candidates. By making use of 4 choices on the second layer, now we have 16 candidates in complete. We then bucket them into ranges from $1–$2, $3–$4, $5–$6, and $7–$8, and solely preserve essentially the most scrumptious burger inside every of the buckets, i.e., 4 candidates. Then, for these 4 candidates, we construct 16 candidates utilizing the pre-selected choices for the primary two layers and 4 choices for every candidate for the third layer. We bucket them once more, choose the burgers throughout the price range vary, and preserve the most effective one. |
Experimental outcomes
When evaluating NAS algorithms, we consider the next metrics:
- Quality: What is essentially the most correct mannequin that the algorithm can discover?
- Stability: How steady is the number of a superb mannequin? Can high-accuracy fashions be persistently found in consecutive trials of the algorithm?
- Efficiency: How lengthy does it take for the algorithm to discover a high-accuracy mannequin?
We consider our algorithm on the usual benchmark NATS-Bench utilizing 100 NAS runs, and we examine in opposition to different NAS algorithms, beforehand described in the NATS-Bench paper: random search, regularized evolution, and proximal coverage optimization. Below, we visualize the variations between these search algorithms for the metrics described above. For every comparability, we report the typical accuracy and variation in accuracy (variation is famous by a shaded area equivalent to the 25% to 75% interquartile vary).
NATS-Bench measurement search defines a 5-layer CNN mannequin, the place every layer can select from eight completely different choices, every with completely different channels on the convolution layers. Our purpose is to search out the most effective mannequin with 50% of the FLOPs required by the biggest mannequin. LayerNAS efficiency stands aside as a result of it formulates the issue in a special means, separating the fee and reward to keep away from looking a major variety of irrelevant mannequin architectures. We discovered that mannequin candidates with fewer channels in earlier layers are likely to yield higher efficiency, which explains how LayerNAS discovers higher fashions a lot quicker than different algorithms, because it avoids spending time on fashions exterior the specified price vary. Note that the accuracy curve drops barely after looking longer as a result of lack of correlation between validation accuracy and check accuracy, i.e., some mannequin architectures with larger validation accuracy have a decrease check accuracy in NATS-Bench measurement search.
We assemble search areas based mostly on MobileNetV2, MobileNetV2 1.4x, MobileNetV3 Small, and MobileNetV3 Large and search for an optimum mannequin architecture beneath completely different #MADDs (variety of multiply-additions per picture) constraints. Among all settings, LayerNAS finds a mannequin with higher accuracy on ImageNet. See the paper for particulars.
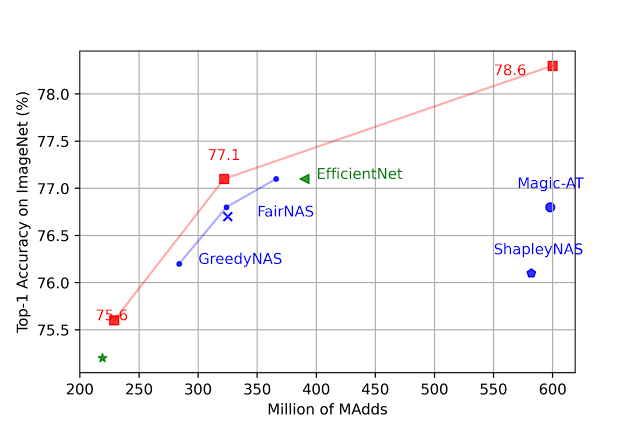 |
| Comparison on fashions beneath completely different #MAdds. |
Conclusion
In this submit, we demonstrated tips on how to reformulate NAS right into a combinatorial optimization drawback, and proposed LayerNAS as an answer that requires solely polynomial search complexity. We in contrast LayerNAS with present in style NAS algorithms and confirmed that it might discover improved fashions on NATS-Bench. We additionally use the tactic to search out higher architectures based mostly on MobileNetV2, and MobileNetV3.
Acknowledgements
We want to thank Jingyue Shen, Keshav Kumar, Daiyi Peng, Mingxing Tan, Esteban Real, Peter Young, Weijun Wang, Qifei Wang, Xuanyi Dong, Xin Wang, Yingjie Miao, Yun Long, Zhuo Wang, Da-Cheng Juan, Deqiang Chen, Fotis Iliopoulos, Han-Byul Kim, Rino Lee, Andrew Howard, Erik Vee, Rina Panigrahy, Ravi Kumar and Andrew Tomkins for his or her contribution, collaboration and recommendation.

