Modern neural networks have achieved spectacular efficiency throughout a wide range of functions, equivalent to language, mathematical reasoning, and imaginative and prescient. However, these networks typically use giant architectures that require a number of computational sources. This could make it impractical to serve such fashions to customers, particularly in resource-constrained environments like wearables and smartphones. A extensively used strategy to mitigate the inference prices of pre-trained networks is to prune them by eradicating a few of their weights, in a manner that doesn’t considerably have an effect on utility. In normal neural networks, every weight defines a connection between two neurons. So after weights are pruned, the enter will propagate by means of a smaller set of connections and thus requires much less computational sources.
 |
| Original network vs. a pruned network. |
Pruning strategies may be utilized at totally different levels of the network’s coaching course of: publish, throughout, or earlier than coaching (i.e., instantly after weight initialization). In this publish, we concentrate on the post-training setting: given a pre-trained network, how can we decide which weights ought to be pruned? One common technique is magnitude pruning, which removes weights with the smallest magnitude. While environment friendly, this technique doesn’t instantly think about the impact of eradicating weights on the network’s efficiency. Another common paradigm is optimization-based pruning, which removes weights based mostly on how a lot their removing impacts the loss operate. Although conceptually interesting, most present optimization-based approaches appear to face a critical tradeoff between efficiency and computational necessities. Methods that make crude approximations (e.g., assuming a diagonal Hessian matrix) can scale properly, however have comparatively low efficiency. On the opposite hand, whereas strategies that make fewer approximations are likely to carry out higher, they seem like a lot much less scalable.
In “Fast as CHITA: Neural Network Pruning with Combinatorial Optimization”, offered at ICML 2023, we describe how we developed an optimization-based strategy for pruning pre-trained neural networks at scale. CHITA (which stands for “Combinatorial Hessian-free Iterative Thresholding Algorithm”) outperforms present pruning strategies by way of scalability and efficiency tradeoffs, and it does so by leveraging advances from a number of fields, together with high-dimensional statistics, combinatorial optimization, and neural network pruning. For instance, CHITA may be 20x to 1000x sooner than state-of-the-art strategies for pruning ResNet and improves accuracy by over 10% in lots of settings.
Overview of contributions
CHITA has two notable technical enhancements over common strategies:
- Efficient use of second-order info: Pruning strategies that use second-order info (i.e., referring to second derivatives) obtain the cutting-edge in lots of settings. In the literature, this info is often utilized by computing the Hessian matrix or its inverse, an operation that could be very troublesome to scale as a result of the Hessian measurement is quadratic with respect to the variety of weights. Through cautious reformulation, CHITA makes use of second-order info with out having to compute or retailer the Hessian matrix explicitly, thus permitting for extra scalability.
- Combinatorial optimization: Popular optimization-based strategies use a easy optimization approach that prunes weights in isolation, i.e., when deciding to prune a sure weight they don’t consider whether or not different weights have been pruned. This might result in pruning essential weights as a result of weights deemed unimportant in isolation might turn out to be essential when different weights are pruned. CHITA avoids this challenge through the use of a extra superior, combinatorial optimization algorithm that takes under consideration how pruning one weight impacts others.
In the sections beneath, we focus on CHITA’s pruning formulation and algorithms.
A computation-friendly pruning formulation
There are many attainable pruning candidates, that are obtained by retaining solely a subset of the weights from the unique network. Let okay be a user-specified parameter that denotes the variety of weights to retain. Pruning may be naturally formulated as a best-subset choice (BSS) downside: amongst all attainable pruning candidates (i.e., subsets of weights) with solely okay weights retained, the candidate that has the smallest loss is chosen.
 |
| Pruning as a BSS downside: amongst all attainable pruning candidates with the identical whole variety of weights, the most effective candidate is outlined because the one with the least loss. This illustration reveals 4 candidates, however this quantity is mostly a lot bigger. |
Solving the pruning BSS downside on the unique loss operate is mostly computationally intractable. Thus, much like earlier work, equivalent to OBD and OBS, we approximate the loss with a quadratic operate through the use of a second-order Taylor collection, the place the Hessian is estimated with the empirical Fisher info matrix. While gradients may be usually computed effectively, computing and storing the Hessian matrix is prohibitively costly as a result of its sheer measurement. In the literature, it is not uncommon to deal with this problem by making restrictive assumptions on the Hessian (e.g., diagonal matrix) and likewise on the algorithm (e.g., pruning weights in isolation).
CHITA makes use of an environment friendly reformulation of the pruning downside (BSS utilizing the quadratic loss) that avoids explicitly computing the Hessian matrix, whereas nonetheless utilizing all the data from this matrix. This is made attainable by exploiting the low-rank construction of the empirical Fisher info matrix. This reformulation may be seen as a sparse linear regression downside, the place every regression coefficient corresponds to a sure weight within the neural network. After acquiring an answer to this regression downside, coefficients set to zero will correspond to weights that ought to be pruned. Our regression information matrix is (n x p), the place n is the batch (sub-sample) measurement and p is the variety of weights within the authentic network. Typically n << p, so storing and working with this information matrix is rather more scalable than widespread pruning approaches that function with the (p x p) Hessian.
 |
| CHITA reformulates the quadratic loss approximation, which requires an costly Hessian matrix, as a linear regression (LR) downside. The LR’s information matrix is linear in p, which makes the reformulation extra scalable than the unique quadratic approximation. |
Scalable optimization algorithms
CHITA reduces pruning to a linear regression downside underneath the next sparsity constraint: at most okay regression coefficients may be nonzero. To get hold of an answer to this downside, we think about a modification of the well-known iterative laborious thresholding (IHT) algorithm. IHT performs gradient descent the place after every replace the next post-processing step is carried out: all regression coefficients outdoors the Top-okay (i.e., the okay coefficients with the biggest magnitude) are set to zero. IHT usually delivers an excellent answer to the issue, and it does so iteratively exploring totally different pruning candidates and collectively optimizing over the weights.
Due to the dimensions of the issue, normal IHT with fixed studying price can undergo from very sluggish convergence. For sooner convergence, we developed a brand new line-search technique that exploits the issue construction to discover a appropriate studying price, i.e., one which results in a sufficiently giant lower within the loss. We additionally employed a number of computational schemes to enhance CHITA’s effectivity and the standard of the second-order approximation, resulting in an improved model that we name CHITA++.
Experiments
We examine CHITA’s run time and accuracy with a number of state-of-the-art pruning strategies utilizing totally different architectures, together with ResNet and MobileNet.
Run time: CHITA is rather more scalable than comparable strategies that carry out joint optimization (versus pruning weights in isolation). For instance, CHITA’s speed-up can attain over 1000x when pruning ResNet.
Post-pruning accuracy: Below, we examine the efficiency of CHITA and CHITA++ with magnitude pruning (MP), Woodfisher (WF), and Combinatorial Brain Surgeon (CBS), for pruning 70% of the mannequin weights. Overall, we see good enhancements from CHITA and CHITA++.
 |
| Post-pruning accuracy of varied strategies on ResNet20. Results are reported for pruning 70% of the mannequin weights. |
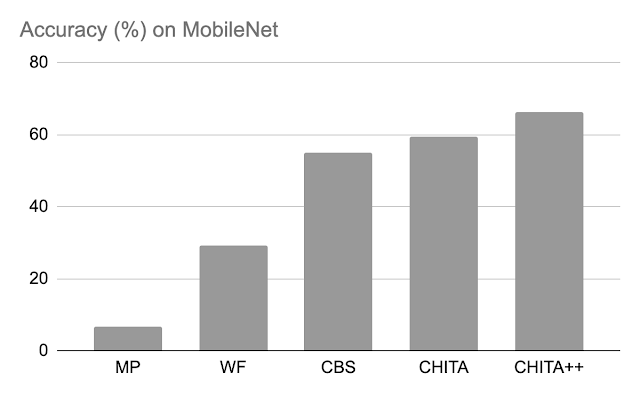 |
| Post-pruning accuracy of varied strategies on MobileNet. Results are reported for pruning 70% of the mannequin weights. |
Next, we report outcomes for pruning a bigger network: ResNet50 (on this network, a few of the strategies listed within the ResNet20 determine couldn’t scale). Here we examine with magnitude pruning and M-FAC. The determine beneath reveals that CHITA achieves higher check accuracy for a variety of sparsity ranges.
 |
| Test accuracy of pruned networks, obtained utilizing totally different strategies. |
Conclusion, limitations, and future work
We offered CHITA, an optimization-based strategy for pruning pre-trained neural networks. CHITA presents scalability and aggressive efficiency by effectively utilizing second-order info and drawing on concepts from combinatorial optimization and high-dimensional statistics.
CHITA is designed for unstructured pruning by which any weight may be eliminated. In concept, unstructured pruning can considerably cut back computational necessities. However, realizing these reductions in observe requires particular software program (and presumably {hardware}) that help sparse computations. In distinction, structured pruning, which removes complete buildings like neurons, might supply enhancements which can be simpler to realize on general-purpose software program and {hardware}. It can be fascinating to increase CHITA to structured pruning.
Acknowledgements
This work is a part of a analysis collaboration between Google and MIT. Thanks to Rahul Mazumder, Natalia Ponomareva, Wenyu Chen, Xiang Meng, Zhe Zhao, and Sergei Vassilvitskii for his or her assist in making ready this publish and the paper. Also because of John Guilyard for creating the graphics on this publish.

